how to find the x intercept of a function

The intercepts of a graph are points at which the graph crosses the axes. The x-intercept is the point at which the graph crosses the x-axis. At this point, the y-coordinate is zero. The y-intercept is the point at which the graph crosses the y-axis. At this point, the x-coordinate is zero.

To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y. For example, lets find the intercepts of the equation [latex]y=3x - 1[/latex].

To find the x-intercept, set [latex]y=0[/latex].

[latex]\begin{array}{ll}y=3x - 1\hfill & \hfill \\ 0=3x - 1\hfill & \hfill \\ 1=3x\hfill & \hfill \\ \frac{1}{3}=x\hfill & \hfill \\ \left(\frac{1}{3},0\right)\hfill & x\text{-intercept}\hfill \end{array}[/latex]

To find the y-intercept, set [latex]x=0[/latex].

[latex]\begin{array}{l}y=3x - 1\hfill \\ y=3\left(0\right)-1\hfill \\ y=-1\hfill \\ \left(0,-1\right)y\text{-intercept}\hfill \end{array}[/latex]

We can confirm that our results make sense by observing a graph of the equation as in Figure 10. Notice that the graph crosses the axes where we predicted it would.

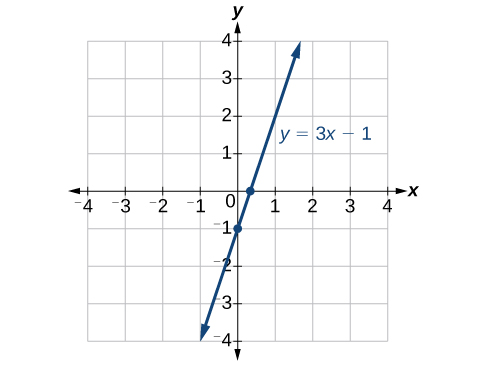
This is an image of a line graph on an x, y coordinate plane. The x and y-axis range from negative 4 to 4. The function y = 3x – 1 is plotted on the coordinate plane

Figure 12

How To: Given an equation, find the intercepts.

Find the x-intercept by setting [latex]y=0[/latex] and solving for [latex]x[/latex].
Find the y-intercept by setting [latex]x=0[/latex] and solving for [latex]y[/latex].

Example 4: Finding the Intercepts of the Given Equation

Find the intercepts of the equation [latex]y=-3x - 4[/latex]. Then sketch the graph using only the intercepts.

Solution

Set [latex]y=0[/latex] to find the x-intercept.

[latex]\begin{array}{l}y=-3x - 4\hfill \\ 0=-3x - 4\hfill \\ 4=-3x\hfill \\ -\frac{4}{3}=x\hfill \\ \left(-\frac{4}{3},0\right)x\text{-intercept}\hfill \end{array}[/latex]

Set [latex]x=0[/latex] to find the y-intercept.

[latex]\begin{array}{l}y=-3x - 4\hfill \\ y=-3\left(0\right)-4\hfill \\ y=-4\hfill \\ \left(0,-4\right)y\text{-intercept}\hfill \end{array}[/latex]

Plot both points, and draw a line passing through them as in Figure 11.

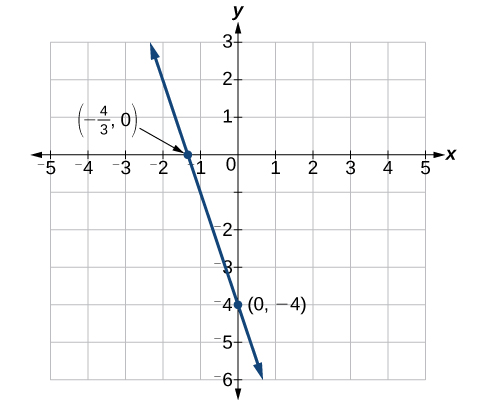
This is an image of a line graph on an x, y coordinate plane. The x-axis ranges from negative 5 to 5. The y-axis ranges from negative 6 to 3. The line passes through the points (-4/3, 0) and (0, -4).

Figure 13

Try It 1

Find the intercepts of the equation and sketch the graph: [latex]y=-\frac{3}{4}x+3[/latex].

Solution